Matrix-Verschlüsselung: Anleitung

Es geht hierbei um die Verschlüsselung von Text mit Hilfe von Matrixprodukten.
Es ist nicht gerade einfach aber weitaus sicherer als gängige, von Hand durchführbare Verschlüsselungsverfahren.
Die eigentlichen Rechenschritte sind zumeist einfach mit Kopfrechnen zu bewerkstelligen.
Zu diesem Verschlüsselungsverfahren muß man erst ein kleines Beispiel haben.
Zuerst aber allgemeine Regeln.

Das Produkt zweier Matrizen kann nur dann gebildet werden, wenn die Spaltenanzahl der 1. Matrix gleich der Zeilenanzahl der zweiten Matrix ist.

So ist zum Beispiel die Multiplikation der Matrizen:

D · C = · 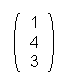mit dem Ergebnis 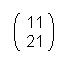möglich,
aber die Multiplikation von C · D = 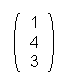· nicht möglich, da hier die Spaltenanzahl der 1. Matrix kleiner als die Zeilenanzahl der 2. Matrix ist.

Zu einer Matrix A ist die inverse Matrix A^-1 durch die Eigenschaft erklärt:

A · A^-1 = A^-1 · A = E

Hierbei ist E das neutrale Element der Multiplikation, z.B. gilt E = für die (2;2) Matrizen, also eine Matrix mit zwei Zeilen und zwei Spalten.
Für die (3;3) Matrizen gilt entsprechend:

Also für (n;n) Matrizen gilt demnach:
(n 0 0 0 0 0 ....... 0 n 0 0 0 0 ...... 0 0 n 0 0 0 etc.)

Gesucht ist die inverse Matrix A^-1 zu A =

Wegen der besseren Lesbarkeit verwendet man bei Matrizen mit geringer Anzahl von Elementen verschiedene Buchstaben mit nur einem Index.

Hier wird wieder das Schema A · A^-1 = A^-1 · A = E benutzt. E und A sind bekannt, daraus folgt demnach:

· = <=> = =

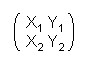Aus der Gleichheit der Matrizen folgt:

X₁ = 1       Y₁ = 0
-1 + 2 · X₂ = 0 <=> X₂ = ½        - 0 + 2 · Y₂ = 1 <=> Y₂ = ½

Also gilt:

A^-1 =


Kommen wir nun zum wirklich interessanten Teil, der Verschlüsselung eines Satzes.

Zuerst noch eine allgemeine Information zu Geheimschriften.

Geheimschriften lassen sich immer dann einfach entziffern, wenn die einzelnen Buchstaben lediglich durch einen anderen ersetzt werden. In diesen Fällen führt eine Untersuchung der Buchstabenhäufigkeit meistens schnell zum Ziel. Hier bieten die Matrizen einen kaum zu knackenden Code. Zunächst erhält jeder zu verschlüsselnde Buchstabe eine Nummer je nach seiner Stellung im Alphabet.

Also.
A = 1, B = 2...... Z = 26

Nun kann man einen beliebigen Satz nehmen, zum Beispiel:

"Big Brother is watching"

Nun muß man sich nur noch entscheiden, ob man eine (2;2) Matrix nehmen will, oder eine komplexere, also größere. Je größer die Matrix, desto sicherer die Verschlüsselung.

Nun, da es noch am einfachsten ist nehme ich besagte (2;2) Matrix.

Ich ordne also den Satz zu Wortpaaren à 4 Buchstaben an:

BIGB ROTH ERIS WATC HING


Nun wird jedem Buchstaben eine Zahl zugeordnet und in eine Matrix gepackt.

Also:



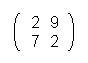
Zum Schluß wird jede dieser Matrizen mit der Verschlüsselungsmatrix U multipliziert.
Zum Beispiel: U = . Diese ist natürlich beliebig austauschbar.

Also erhält man in diesem Beispiel dann:



Nun kann man auch erkennen, dass gleichen Buchstaben nun nicht mehr gleiche Zahlen zugeordnet sind. Zum Beispiel das “t”. Es hat einmal die Zahl 76 und dann einmal die Zahl 41.

Um den Sinn des Satzes zurückzuerhalten muß mit der Entschlüsselungsmatrix U^-1 multipliziert werden. (Also die inverse Matrix A^-1)

Das Verfahren ist oben angegeben.
Für die Matrix A = gilt also:

A^-1 = = U^-1

Durch Multiplikation erhält man die alten Matrizen wieder.

Diese Art der Verschlüsselung ist sehr sicher, da jedem, der den Text entschlüsseln will, die Verschlüsselungsmatrix bekannt sein muß. Die Zahl dieser möglichen Matrizen ist unendlich. Daher ist auch eine Entschlüsselung mit Hilfe eines Computers unwahrscheinlich, da sich für jede andere Matrix ein anderer "Text" ergeben kann. Durch Einschränkung der Zahlenwerte, welche nicht größer als 26 sein können schränkt sich die Anzahl der Möglichkeiten zwar etwas ein, aber es gibt trotzdem noch unendlich viele mögliche Matrizen.
Natürlich ist die Verschlüsselung von Text mit entsprechenden Programmen, wie z.B. PGP weitaus einfacher, aber die Verschlüsselung auf dem von mir beschriebenen Weg kann auch mit Papier und Bleistift durchgeführt werden und ist in jedem Fall sicherer als die meisten anderen Verschlüsselungssysteme, welche per Hand durchführbar sind.



Written by [Andi]